报告题目:希尔伯特第16问题及相关研究
报 告 人:李承治教授(北京大学)
报告时间:2024年6月12日下午15:00-16:30
报告地点:腾讯会议(653-167-096)
报告摘要:
D.Hilber 在1900年提出著名的23个数学问题,其中第16问题(后半部分)可陈述为:对给定的整数n ≥ 2和全体n次多项式Pn(x,y),Qn(x,y),平面系统
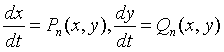
可能具有的极限环最大个数 H(n)=? 如果 H(n)有限,它们可能具有的相互位置如何?
一百二十多年来,有大量研究工作出现,包括我国数学工作者的贡献,促使研究极限环的理论和方法获得很大进展。但就上述问题本身而言取得的成果有限,连n=2的情形尚未解决,因此这个问题被一些知名学者列入本世纪的重大数学问题之一。困难与挑战召唤并激励着有为青年,促使人们去探索研究思想与研究方法的创新。
我们拟对这个问题及其在二次系统、三次系统和一般系统方面的部分重要工作分别做一个简要的介绍。
个人简历:李承治,北京大学教授。多年从事教学与科研,研究方向为微分方程定性理论和动力系统分支理论。1981年以来多次应邀到国内外多所大学访问、参加会议、作学术报告,或开展合作研究,并在美国、加拿大、西班牙的4所大学讲授过本科生或研究生课程。与国内外同行合作在高等教育出版社和科学出版社出版本科生与研究生教材三本,在英国剑桥大学出版社和Birkhäuser Verlag出版社出版专著各一本,发表学术论文80多篇。长期主持或参加国家自然科学基金重点项目或面上项目,教育部博士点基金项目,曾是国家自然科学基金委员会数学评审组成员,教育部高校理科数学与力学教学指导委员会基础数学组成员。1991年获国家教委、国务院学位委员会授予“有突出贡献的中国博士”称号,1993年获北京大学第四届科技成果一等奖,《向量场分支的几个问题》于1994年获国家教委科技进步奖二等奖,1996年获教委优秀教材一等奖(第二完成人),2005年获北京市优秀教学成果一等奖(第一完成人)。2019年获首届北京大学离退休教职工学术贡献奖特等奖。
